TUCWave

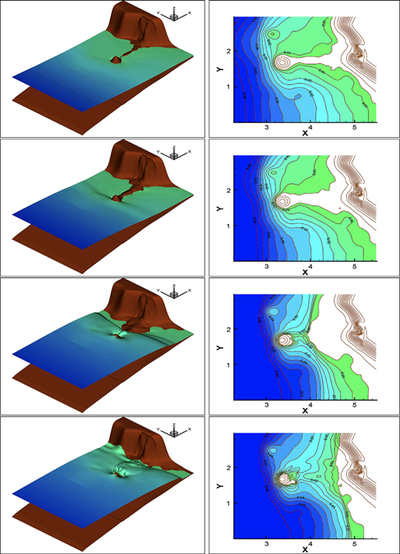
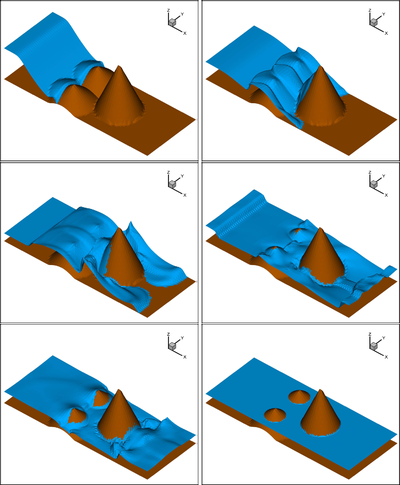
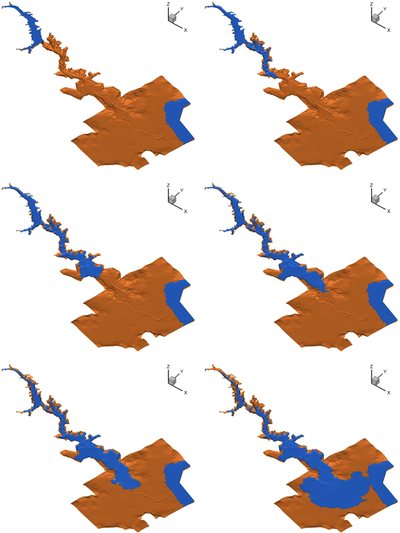
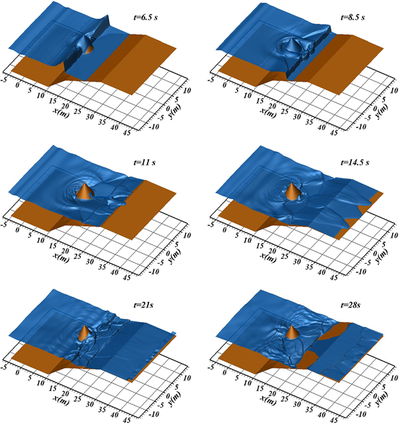
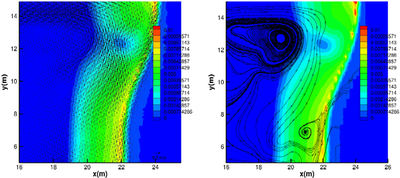
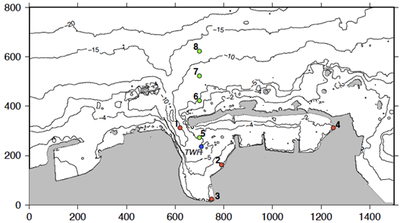
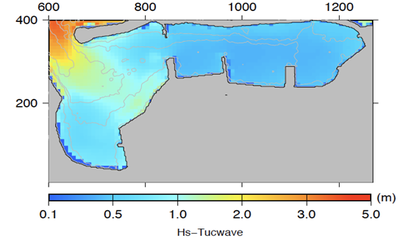
TUCWave: A novel Fortran Planform that advances a step ahead the methodology of the solution of dispersive wave models, which account for the study of near-shore processes. TUCWave uses a high-order well-balanced unstructured finite volume (FV) scheme on triangular meshes for modeling weakly nonlinear and weakly dispersive water waves over varying bathymetries, as described by the 2D depth-integrated extended Boussinesq equations of Nwogu (1993), rewritten in conservation law form. The model has the option of using only its nonlinear shallow water solver (without the dispersive terms). The FV scheme numerically solves the conservative form of the equations following the median dual node-centered approach, for both the advective and dispersive part of the equations. The code developed follows an efficient edge-based structured technique. For the advective fluxes, the scheme utilizes an approximate Riemann solver along with a well-balanced topography source term up-winding. Higher order accuracy in space and time is achieved through a MUSCL-type reconstruction technique and through a strong stability preserving explicit Runge-Kutta time stepping. Special attention is given to the accurate numerical treatment of moving wet/dry fronts, wave breaking and boundary conditions. Furthermore, the model has applied to several examples of wave propagation over variable topographies and the computed solutions are compared to experimental data.

References:

I.K. Nikolos, A.I. Delis, "An unstructured node-centered finite volume scheme for shallow water flows with wet/dry fronts over complex topography", Computer Methods in Applied Mechanics and Engineering, 198, pp. 3723-3750, 2009. https://doi.org/10.1016/j.cma.2009.08.006

A.I. Delis, I.K. Nikolos, M. Kazolea, "Performance and comparison of cell-centered and node-centered unstructured finite volume discretizations for shallow water free surface flows", Archives of Computational Methods in Engineering, 18 (1), pp. 57-118, 2011. https://doi.org/10.1007/s11831-011-9057-6

M. Kazolea, A.I. Delis, I.K. Nikolos, C.E. Synolakis, "An unstructured finite volume numerical scheme for extended 2D Boussinesq-type models", Coastal Engineering, 69, pp. 42-66, 2012. https://doi.org/10.1016/j.coastaleng.2012.05.008

M. Kazolea, A.I. Delis, C.E. Synolakis, "Numerical treatment of wave breaking on unstructured finite volume approximations for extended Boussinesq-type equations", Journal of Computational Physics, 271, pp. 281-305, 2014. https://doi.org/10.1016/j.jcp.2014.01.030

M. Kazolea, A.I. Delis, "Irregular wave propagation with a 2DH Boussinesq-type model and an unstructured finite volume scheme", European Journal of Mechanics - B/Fluids, 72, pp. 432-448, 2018. https://doi.org/10.1016/j.euromechflu.2018.07.009

Numerical Applications and Simulations